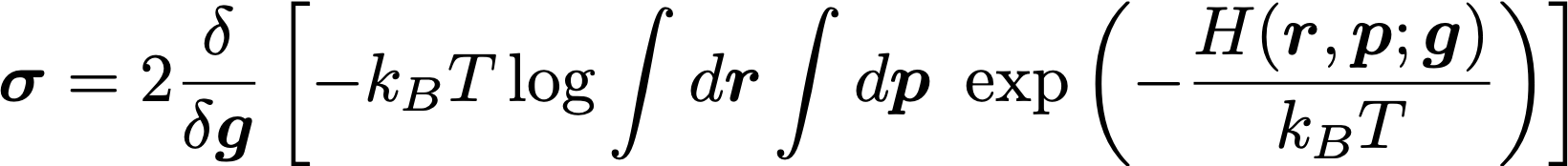Alejandro Torres-Sánchez, Juan M Vanegas, Marino Arroyo. Journal of the Mechanics and Physics of Solids 93, 224-239 (2016).
We revisit the derivation of the microscopic stress, linking the statistical mechanics of particle systems and continuum mechanics. The starting point in our geometric derivation is the Doyle–Ericksen formula, which states that the Cauchy stress tensor is the derivative of the free-energy with respect to the ambient metric tensor and which follows from a covariance argument. Thus, our approach to define the microscopic stress tensor does not rely on the statement of balance of linear momentum as in the classical Irving–Kirkwood–Noll approach. Nevertheless, the resulting stress tensor satisfies balance of linear and angular momentum. Furthermore, our approach removes the ambiguity in the definition of the microscopic stress in the presence of multibody interactions by naturally suggesting a canonical and physically motivated force decomposition into pairwise terms, a key ingredient in this theory. As a result, our approach provides objective expressions to compute a microscopic stress for a system in equilibrium and for force-fields expanded into multibody interactions of arbitrarily high order. We illustrate the proposed methodology with molecular dynamics simulations of a fibrous protein using a force-field involving up to 5-body interactions.