Waleed Mirza, Alejandro Torres-Sánchez, Guillermo Vilanova, Marino Arroyo
Abstract
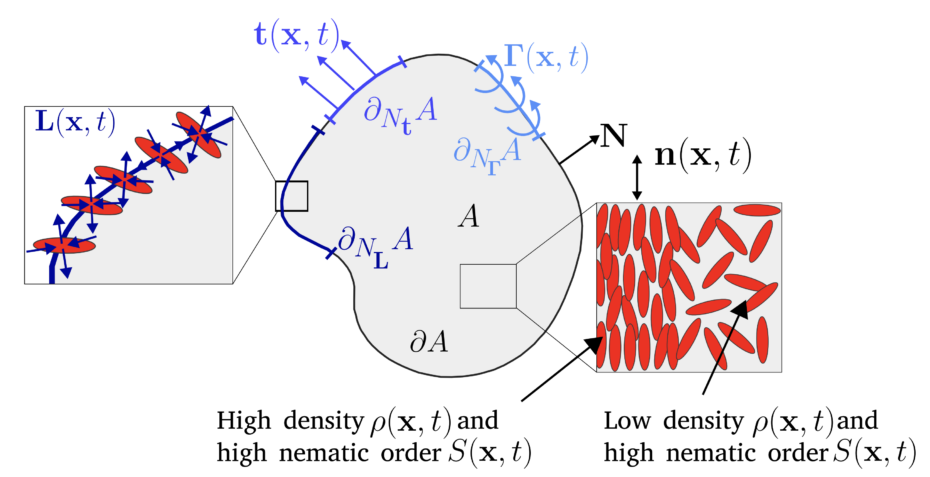
The structure and dynamics of important biological quasi-two-dimensional systems, ranging from cytoskeletal gels to tissues, are controlled by nematic order, defects and activity. Continuum hydrodynamic descriptions combined with numerical simulations have been used to understand such complex systems, but the physical interpretation of different active nematic models and their applicability to specific systems is often unclear. For instance, most works rely on theories for incompressible liquid crystals but important active 2D nematic systems are compressible due to density variations or turnover. Here, we propose a theoretical and computational framework for possibly compressible and density-dependent 2D active nematic systems. This framework is based on Onsager’s variational formalism to irreversible thermodynamics, according to which the dynamics result from a competition between free-energy release, dissipation and activity. We particularize this framework to recover a standard incompressible active nematic model and further formulate an alternative model for density-dependent active nemato-hydrodynamics. We show that the variational principle enables a direct and transparent derivation not only of the governing equations, but also of the finite element numerical scheme. We exercise this model in two representative examples of active nematodynamics relevant to the actin cytoskeleton during wound healing and to the dynamics of confined colonies of elongated cells.