Ariadna Marín-Llauradó, Sohan Kale, Adam Ouzeri, Raimon Sunyer, Alejandro Torres-Sánchez, Ernest Latorre, Manuel Gómez-González, Pere Roca-Cusachs, Marino Arroyo, Xavier Trepat
Abstract
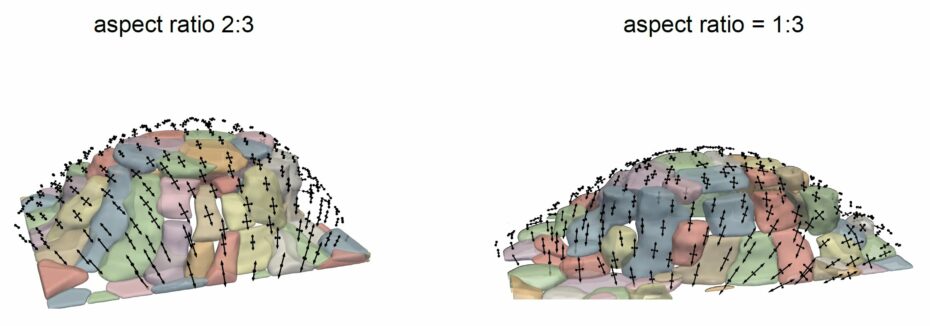
The function of organs such as lungs, kidneys and mammary glands relies on the three-dimensional geometry of their epithelium. To adopt shapes such as spheres, tubes and ellipsoids, epithelia generate mechanical stresses that are generally unknown. Here we engineered curved epithelial monolayers of controlled size and shape and mapped their state of stress. We designed pressurized epithelia with circular, rectangular and ellipsoidal footprints. We developed a computational method to map the stress tensor in these epithelia. This method establishes a direct correspondence between epithelial shape and mechanical stress without assumptions of material properties. In epithelia with spherical geometry spanning more than one order of magnitude in radius, we show that stress weakly increases with areal strain in a size-independent manner. In epithelia with rectangular and ellipsoidal cross-section we found pronounced stress anisotropies consistent with the asymmetric distribution of tractions measured at the cell-substrate contact line. In these anisotropic profiles, cell shape tended to align with the direction of maximum principal stress but this alignment was non-universal and depended on epithelial geometry. Besides interrogating the fundamental mechanics of epithelia over a broad range of sizes and shapes, our approach will enable a systematic study of how geometry and stress influence epithelial fate and function in three-dimensions.