Alejandro Torres-Sánchez, Daniel Santos-Oliván, Marino Arroyo. Journal of Computational Physics 405, 109168 (2020).
Abstract
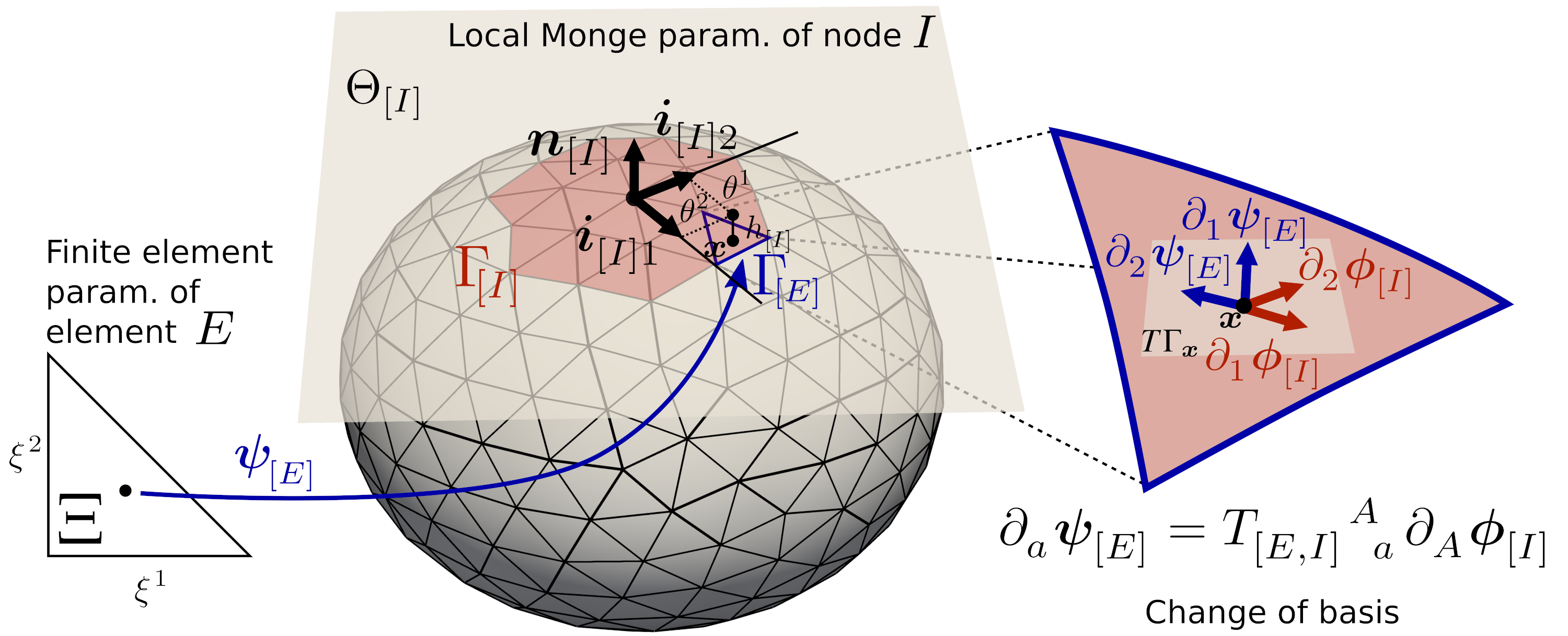
We introduce a new method, the Local Monge Parametrizations (LMP) method, to approximate tensor fields on general surfaces given by a collection of local parametrizations, eg~ as in finite element or NURBS surface representations. Our goal is to use this method to solve numerically tensor-valued partial differential equations (PDE) on surfaces. Previous methods use scalar potentials to numerically describe vector fields on surfaces, at the expense of requiring higher-order derivatives of the approximated fields and limited to simply connected surfaces, or represent tangential tensor fields as tensor fields in 3D subjected to constraints, thus increasing the essential number of degrees of freedom. In contrast, the LMP method uses an optimal number of degrees of freedom to represent a tensor, is general with regards to the topology of the surface, and does not increase the order of the PDEs governing the tensor fields. The main idea is to construct maps between the element parametrizations and a local Monge parametrization around each node. We test the LMP method by approximating in a least-squares sense different vector and tensor fields on simply connected and genus-1 surfaces. Furthermore, we apply the LMP method to two physical models on surfaces, involving a tension-driven flow (vector-valued PDE) and nematic ordering (tensor-valued PDE). The LMP method thus solves the long-standing problem of the interpolation of tensors on general surfaces with an optimal number of degrees of freedom.